
ITパスポートではクリティカルパスが試験範囲に含まれています。
※ITパスポートの試験範囲の詳細は「ITパスポートの試験範囲は広い!変更・拡大されることもあるので要注意」をご覧ください。
クリティカルパスの問題は解き方をしっかりと理解していれば難しくはないので、出題されたら得点のチャンスです。
今回はITパスポートを日本トップレベルに熟知している私ケンジが、ITパスポートで出題されるクリティカルパスとは何かについて解説した後、クリティカルパスに関する問題の解き方を例題でわかりやすく解説します。
最後にはクリティカルパスの練習問題(過去問)も用意しているので、ぜひ最後までお読みください。
ちなみにですが、ITパスポートにはたった10時間の勉強で合格できる方法があります。
これさえあれば限りなく少ない努力で合格に大きく近づきます。
これは私が何年もITパスポートの勉強を続ける中で生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味ある人はぜひ以下のボタンからその方法をチェックしてください。
クリティカルパスはITパスポートの試験範囲!解き方を例題でわかりやすく解説
ITパスポートでは3つの分野(ストラテジ系・マネジメント系・テクノロジ系)から問題が出題されますが、クリティカルパスはマネジメント系で出題される可能性があります。
※それぞれの分野の詳細は「ITパスポートの分野は3つある!分野別評価点・割合は?難しいのはどれ?」をご覧ください。
クリティカルパスとは、プロジェクトにおいて最も時間のかかる経路のことです。
この経路上の作業が遅れるとプロジェクト全体が遅れるため、プロジェクト管理において重視されます。
以下の図においては、A→B→Eの経路がクリティカルパスとなります。全作業を完了するまでに6日間必要です。
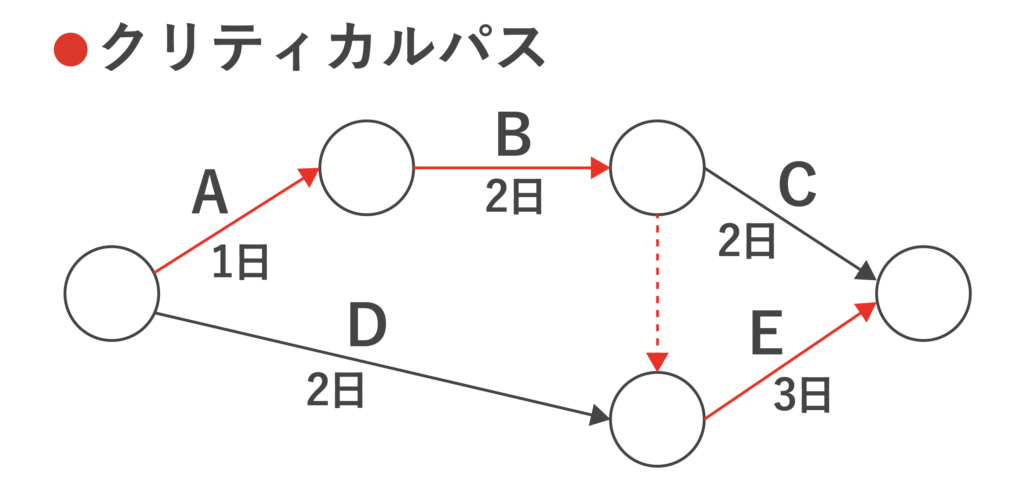
ITパスポートで出題されるクリティカルパスの例題(過去問)は以下です。
【例題(平成23年度過去問)】
図のアローダイアグラムにおいて、作業Bが3日遅れて完了した。全体の遅れを1日にするためには、どの作業を何日短縮すればよいか。
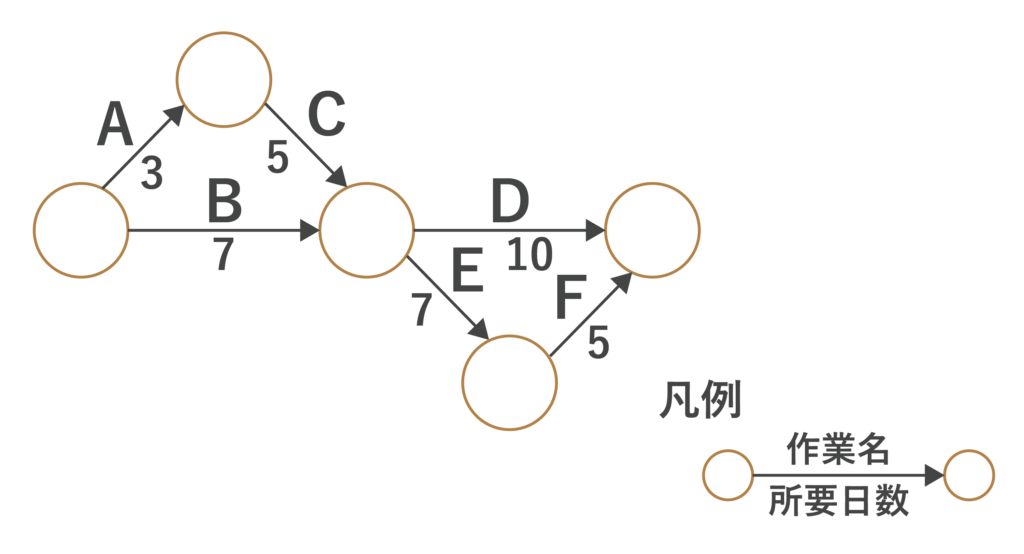
- 作業Cを1日短縮する
- 作業Dを1日短縮する
- 作業Eを1日短縮する
- どの作業も短縮する必要はない
【解答&解説】
正解は3・・・(答)です。
アローダイアグラムとは、作業計画を立てるときに利用する手順を可視化した図のことです。
プロジェクトマネジメントにおいて、タスク(ノード)同士の依存関係を示し、どのタスクをいつまでに開始(または終了)するべきかを視覚的に整理できます。
※アローダイアグラムでは〇をタスク(ノード)といい、タスクを結ぶ矢印をアクティビティといいます。
まずはアローダイアグラム上におけるクリティカルパスを探します。
- A→C→D:18日(3+5+10)
- A→C→E→F:20日(3+5+7+5)
- B→D:17日(7+10)
- B→E→F:19日(7+7+5)
上記より、クリティカルパスはA→C→E→Fの20日だとわかります。
次に作業Bの遅れを考慮して、再度クリティカルパスを探します。
- A→C→D:18日(3+5+10)
- A→C→E→F:20日(3+5+7+5)
- B→D:20日(7+3+10)
- B→E→F:22日(7+3+7+5)
この結果から、クリティカルパスがB→E→Fの22日に変わったことがわかります。
設問では全体の遅れを1日にするとあるので、当初のクリティカルパスの20日に1を足して21日にしたいということがわかります。
つまり、作業B・E・Fのいずれかを1日減らせば21日になります。これに合致する選択肢は3のみです。
🔽 本にも載ってない極秘情報 🔽
ITパスポート:クリティカルパスの練習問題(過去問)
最後に、クリティカルパスの練習問題(ITパスポートの過去問)を3問ご紹介します。
わかりやすく解答・解説も掲載しているので、ITパスポートを受験予定の人はぜひ解いてみてください。
※「ITパスポート練習問題100問無料・答え付き!頻出問題をたくさん掲載」もぜひ合わせてご覧ください。
【練習問題1(令和5年度過去問)】
次のアローダイアグラムに基づき作業を行った結果、作業Dが2日遅延し、作業Fが3日前倒しで完了した。作業全体の所要日数は予定と比べてどれくらい変化したか。
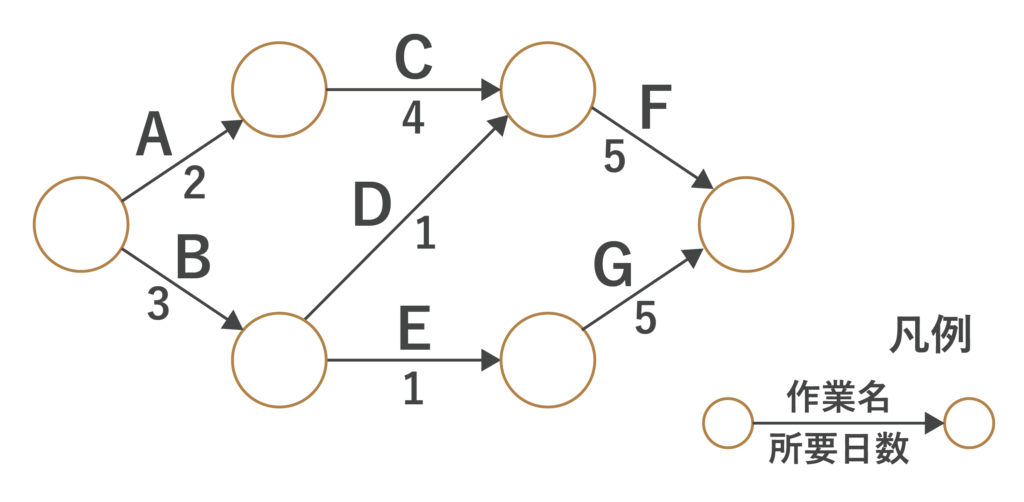
- 3日遅延
- 1日前倒し
- 2日前倒し
- 3日前倒し
【解答&解説】
正解は3・・・(答)です。
もともと予定していた所要日数は、以下3つのパスのうち所要時間が最も多くなるパスの日数です。
- A→C→F:2+4+5=11[日]
- B→D→F:3+1+5=9[日]
- B→E→G:3+1+5=9[日]
よって、もともとは11日間で作業全体が完了する予定だったことがわかります。
このスケジュールから作業Dが2日遅れ、作業Fが3日前倒しで完了すると、
- 作業D:1+2=3[日]
- 作業F:5-3=2[日]
になるので、以上をもとにして再度クリティカルパスを計算すると以下のようになります。
- A→C→F:2+4+2=8[日]
- B→D→F:3+3+2=8[日]
- B→E→G:3+1+5=9[日]
以上より、作業全体が完了するのはB→E→Gが終了する9日目であることがわかります。
よって、もともと予定していた所要日数である11日と比べて2日前倒しになります。
【練習問題2(令和6年度過去問)】
あるプロジェクトの作業間の関係と所要時間がアローダイアグラムで示されている。このアローダイアグラムのBからEの四つの結合点のうち、工程全体の完了時間に影響を与えることなく、その結合点から始まる全ての作業の開始を最も遅らせることができるものはどれか。ここで、各結合点から始まる作業はその結合点に至る作業が全て完了するまで開始できず、作業から次の作業への段取り時間は考えないものとする。
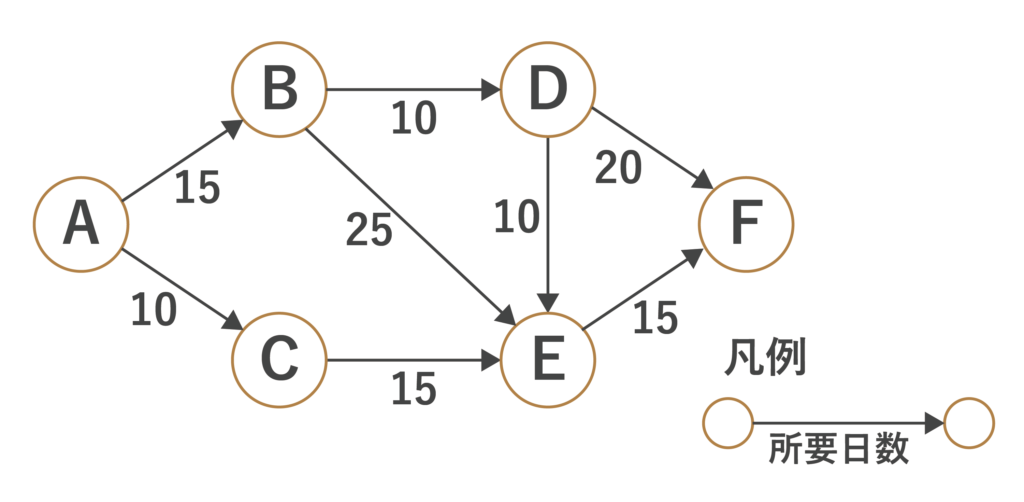
- B
- C
- D
- E
【解答&解説】
正解は2・・・(答)です。
まずはアローダイアグラムにおけるクリティカルパスを考えます。
- A→B→D→F:15+10+20=45[時間]
- A→B→D→E→F:15+10+10+15=50[時間]
- A→B→E→F:15+25+15=55[時間]
- A→C→E→F:10+15+15=40[時間]
以上より、クリティカルパスはA→B→E→F、最短所要時間は55時間であることがわかります。
クリティカルパスはプロジェクトを最短で完了するための工程のことなので、設問の条件である「工程全体の完了時間に影響を与えず、遅らせることができる」のは、クリティカルパス上にない工程でなければなりません。
これを満たすのは結合点CとDの2つのみです。
Cから始まる作業はクリティカルパスであるEからの作業が開始するまでに終わっていれば良いので、最大でA→B→E(40時間)とA→C→E(25時間)の差である15時間を遅らせることが可能です。
一方で、Dから始まる作業はA→B→E(40時間)とA→B→D→E(35時間)の差である5時間しか遅らせることができません。
よって、最も遅らせることができる結合点はCであることがわかります。
【練習問題3(令和4年度過去問)】
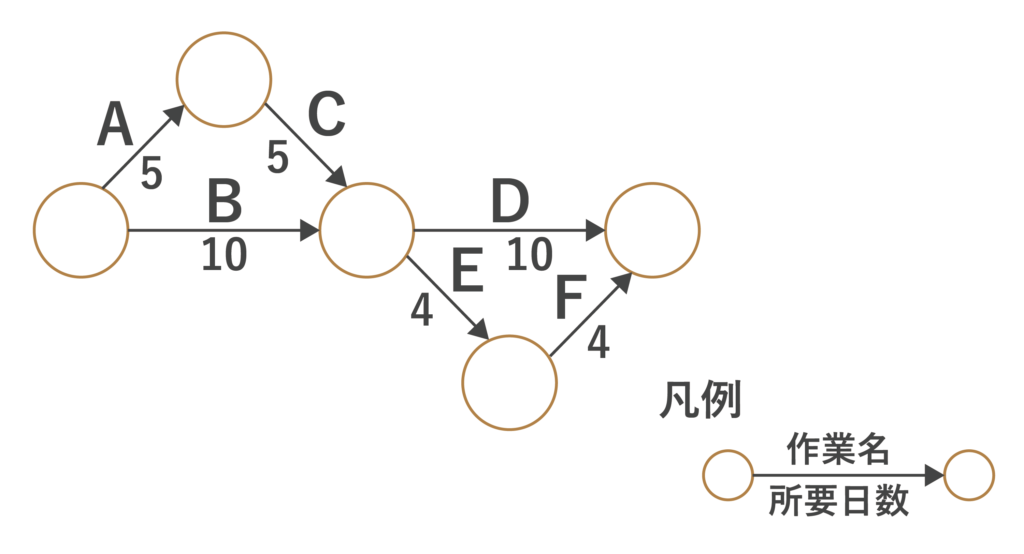
図のアローダイアグラムにおいて、作業Bが2日遅れて完了した。そこで、予定どおりの期間で全ての作業を完了させるために、作業Dに要員を追加することにした。作業Dに当初20名が割り当てられているとき、作業Dに追加する要員は最少で何名必要か。ここで、要員の作業効率は一律である。
- 2
- 3
- 4
- 5
【解答&解説】
正解は4・・・(答)です。
アローダイアグラムにおけるクリティカルパスを考えます。
- A→C→D:5+5+10=20[日]
- A→C→E→F:5+5+4+4=18[日]
- B→D:10+10=20[日]
- B→E→F:10+4+4=18[日]
以上より、クリティカルパスはA→C→DおよびB→Dで、最短所要日数は20日となります。
作業Bが2日遅れたということは、作業Bの完了までに要した日数は12日ということになります。
よって、全体を20日で完了させるためには作業Dを8日で完了させる必要があります。
もともと20人で10日掛かっていた作業(10日×20人=200人日)を8日で完了させるために必要な要員数は、200人日÷8日=25人です。
作業Dに当初割り当てられていた要員数は20人なので、 最少追加人数は25-20=5人となります。
🔽 本にも載ってない極秘情報 🔽
今回はITパスポートのクリティカルパスを取り上げました。
クリティカルパスの問題は解き方さえ理解していればそこまで難しくありません。
ITパスポートを受験予定の人は必ずできるようにしておきましょう。


